A. H. Thiessen proposed thiessen polygon method to show the area of influence of corresponding weather stations in a given area. However, various fields of sciences and social sciences use this technique of regionalisation for research purposes. It is based on division of a given area into polygons of different sizes and shapes. In fact, a researcher uses simple geometric technique to draw the polygons.
How to Draw Thiessen Polygons?
In simple words, thiessen polygons are polygons of different sizes and shapes adjacent to each other drwan around a focal point with the help of geometry. Let us take an example of a catchment area interspersed with many weather stations (see black dots in Fig.1). This exercise is to determine area of influence under each weather stations using thiessen polygon method.
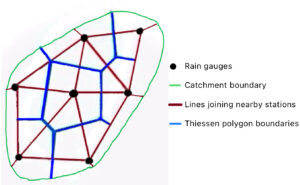
Fig. 1: Thiessen Polygons around weather stations
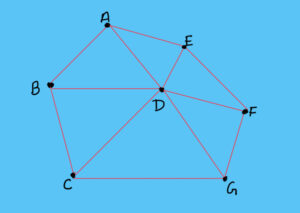
- Firstly, join all the adjacent dots in the region to form the triangles of various shapes and sizes (see maroon lines in Fig.1). Please remember that one has to join the nearest adjacent dots only. Sometimes, a case arises where we get a quadrilateral. In that case, we should not draw diagonals in that quadrilateral to form four triangles. We have to draw one diagonal which is shorter (Fig.2). In Fig. 2, see points A, B, C and D. We have connected them to form a quadrilateral but we have drawn the shorter diagonal BD to form triangles instead of AC. Similar is the case of quadrilateral ADFE. In this manner we get triangulation of area which fulfils Delaunay Criterion.
- Secondly, locate the center points on all the sides of all the triangles (Fig.1).
- Thirdly, draw perpendiculars from all the center points up to the point where other perpendiculars intersect them (see blue lines in Fig. 1).
- Lastly, erase all the sides of triangles. The leftover perpendiculars will act as the boundaries of the regions or area of influence.
Conclusion
From the above discussion, one can conclude that thiessen polygon method is a simple geometric technique to demarcate regions in an isotropic plain. Therefore, this method ignores the various geographic and geomorphic features which affect the regional boundaries. Hence, one should use this method with caution while understanding its limitations.
Kulwinder Singh is an alumni of Jawaharlal Nehru University, New Delhi and working as Assistant Professor of Geography at Pt. C.L.S. Government College, Kurukshetra University. He is a passionate teacher and avid learner.
